
Courtesy http://aerospacescholars.jsc.nasa.gov/HAS/cirr/ss/2/4.cfm

Courtesy http://aerospacescholars.jsc.nasa.gov/HAS/cirr/ss/2/4.cfm
Johannes Kepler (1571-1630)
Johannes Kepler and his contemporary, Galileo, made an assault on the Ptolemaic system which finalized the astronomical revolution in favor of the Copernican model. Kepler spent over 25 years analyzing Tycho's data ... attempting to unlock the secrets it contained. Although Kepler lacked the observational skills of an astronomer, he was diligent and a brilliant mathematician. His attempts to find order in this data led Kepler down many failed paths. At one point, he was convinced that the orbits of the five planets were somehow related to the five perfect geometric solids known to the Greeks (which included the cube and the tetrahedron). They were not! He spent years analyzing patterns in music looking for the "harmony of the spheres" as if proportions of the solar system were connected to musical scales. They were not! Kepler was not afraid to "look outside the box" and test new thoughts. He eventually found success when he abandoned the "perfect" shape of the Greeks - the circle and looked at the ellipse. Even the ancient Greeks knew of ellipses, but Kepler was the first to apply it to planetary orbits.
An ellipse is actually quite easy to make. All you need is a loop of string and two tacks. Wrap the loop around the tacks, pull the string to pick up the slack, and trace (see the animation below). Algebra books define an ellipse as follows:
An ellipse is the set of all points ( x , y ) on the plane such that the sum of the distances from ( x , y ) to two fixed points (foci) is some constant.
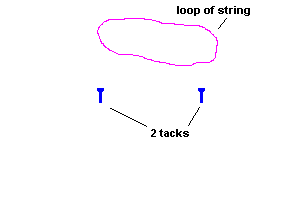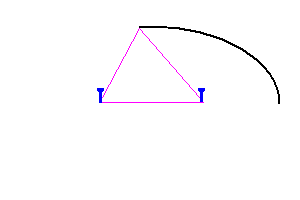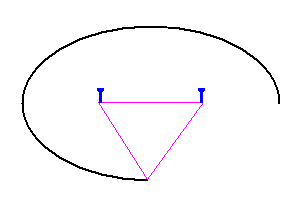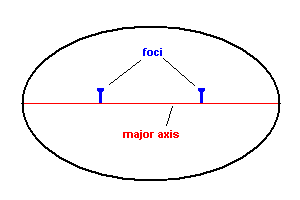
How to draw an ellipse (animation)
If possible, view this 4 MB video in .mp4 format demonstrating how to draw an ellipse - click here.
The tacks define the focal points (foci) and the long "diameter" line (which goes through the foci) is known as the major axis. Half this distance is known as the semi-major axis and is given the symbol "a" in most all books.
Kepler used Tycho's data to construct his first law of planetary motion which states:
Kepler's First Law of Planetary Motion: Planets travel in elliptical orbits with the sun at one of the focal points of the ellipse.
Kepler never tries to explain why the planets travel in this orbit ... he was only interested in determining the orbital shape which fit best with the data provided by Tycho.
Once we accept this law, we are faced with some new challenges. For example, since the distance between Earth and sun are constantly changing, we need to re-define an astronomical unit, and we need to introduce some new terms as well.
Perihelion is the point in a planet's orbit when it is physically closest to the sun. The Earth crosses its perihelion each year around January 3.
Aphelion is the point in a planet's orbit when it is physically farthest from the sun. The Earth crosses its aphelion each year around July 3.
This might seem like a typo! Aren't we cold in Milwaukee on January 3rd? If you recall, we get our seasons because of a 23˝ degree tilt (see material in unit 1). The fact is, the orbit of Earth (to the naked eye) is very nearly a circle. Ellipses can come in many different sizes and shapes. Imagine we repeat the animation above with the same loop of string but move the two tacks further apart. This would produce a "flatter" shape. The closer the two tacks appear, the "rounder" the ellipse becomes. A circle is actually a special variation of the ellipse where the two foci coincide at the center. Mathematicians use the term eccentricity to refer to the shape of the ellipse.
Eccentricity is expressed as a unit-less number (designated as "e") which ranges from e=0 for a perfect circle to e=1 which is a straight line. The orbit of Earth has an eccentricity of .0167 which should tell you that it is very nearly a circle. This is probably a very good thing for us since life on our planet might not be possible if our distance to the sun varied by a considerable amount. The orbit of Mercury has an eccentricity of about .2, Pluto is about .24 and many of the periodic comets which orbit the sun do so with eccentricities over .95 (very cigar shaped).
The Astronomical Unit (re-defined) - Since Earth-sun distance varies from day to day, astronomers look at the average distance Earth is from the sun. This is taken as the semi-major axis of orbit (or "a"). This is approximately 92,900,000 miles (although Kepler never knew this). We vary about ±1,500,000 miles from this at aphelion and perihelion.
When you look up the distance any planet, asteroid, comet, etc is from the sun (on a chart), you will always be given the average distance (semi-major axis) of its orbit. However, astronomy software is capable of calculating the real-time distance if it is needed.
In 1912, Serbian scientist Milutin Milankovitch offered a theory to explain why we have been going through cycles of "ice ages" over the past several million years. He suggests that changes in the eccentricity of the earth's orbit (along with changes in our tilt) could produce the proper conditions to trigger an "ice age". Recently some scientists offered another astronomical hypothesis, but not the one suggested by Milankovitch. This new hypothesis suggests that Earth "bobs" up and down slightly off the ecliptic plane ... thereby encountering more space dust and debris which affects the climate. Either way, the way Earth moves as it orbits the sun may be the cause of these cycles of glaciations.
To honor one of their greatest scientists, Isaac Newton, Great Britain placed his image on the back of the Pound Note. They even added some transcripts from his works, but asked a printer to embellish the drawing. He erroneously placed the sun at the center of the ellipse and not at one of the focal points. If you have any of this "scientifically flawed" money, send it to me for proper disposal.
Kepler discovered this law (and the ones to follow) for planets orbiting the sun. However, all of Kepler's Laws apply to any two bodies in a gravitational dance. For example, the moon orbits Earth in an ellipse. The only thing that changes is a slight change in terminology. When the moon is closest to Earth is not called perihelion but perigee, and when it is furthest from Earth we call it apogee instead of aphelion.
Kepler noticed that the speed of a planet changes as it moves along the ellipse. He found a planet would move the fastest when it was at perihelion and slowest at aphelion (see the animation below).
Changing speed of a planet (animation)
Being a mathematician, he needed a quantitative way of expressing this idea which is indicated in his second law ... known as the Law of Areas.
Kepler's Second Law of Planetary Motion: As a planet moves in its elliptical path, it will sweep out equal area in equal intervals of time.
What's that you say? The animation below should help clarify this statement.
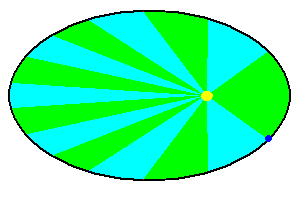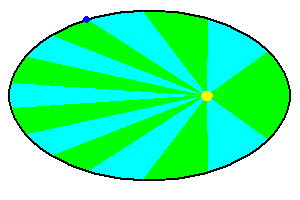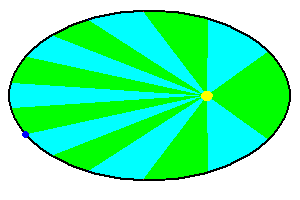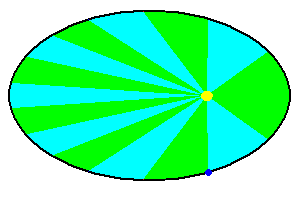
Kepler's Law of Areas (animation)
As a planet moves, it creates tiny "pie shaped wedges" indicated in green and blue (above). Kepler found that if the time needed to create these wedges were equal, so were the areas. This certainly doesn't sound like you are trying to describe the changing speed of a planet ... but in fact you are! Think of these little wedges as if they were triangles ... all with equal areas.
If a planet is near its perihelion, the triangle has a short height (distance to the sun) but a wide base (distance along the circumference). If the area is to remain the same, at aphelion, the much longer height (distance to the sun) has to be compensated by having a much shorter base (distance along the circumference). That can only happen if the planet is moving slower. By describing the law in this manner, Kepler could predict where a planet should be at any specific time and describe how fast it was going. He did not have any clue why the planet behaved this way (the laws of physics as we understand them did not come until Newton).
Let's fast forward a few decades and see why planets behave this way. A planet moves under the influence of gravity, and you all have a "common sense" idea how this works in the real world. If you take a ride on a roller coaster, you know that it goes fast at the bottom and slow at the top. A physicist would describe this in terms of energy - potential and kinetic.
Potential energy is "stored energy" due to an objects position or height in a gravitational field. An apple on the tree has energy because it is some distance from the ground. Once the apple begins to fall, it loses this potential energy and picks up speed (or kinetic energy). It is a simple transfer of energy from one form to another. You experience this when you ride the roller coaster. You know that when you reach the bottom of the track, you are going the fastest ... and then gradually lose speed as you move back up (losing kinetic energy and gaining potential energy back). Planets are constantly moving energy between these two forms as they move in their orbits. At perihelion, a planet has its maximum kinetic energy and minimum potential energy ... the reverse is true at aphelion.
In the last unit, an ancient Greek named Hipparchus discovered that the sun appears to move with changing speed as it moved along the ecliptic. Can you now see why this happens? Click here if you can't figure it out.
Finally, Kepler noticed that planets closer to the sun had shorter sidereal periods. As you looked to more distant planets, the sidereal periods increased. Here is a list of orbital data for the five known planets (and Earth):
| Planet | a Semi-Major Axis (AU) | P Sidereal Period (Earth years) |
| Mercury | .387 | .2408 |
| Venus | .723 | .6152 |
| Earth | 1.000 | 1.000 |
| Mars | 1.524 | 1.881 |
| Jupiter | 5.204 | 11.86 |
| Saturn | 9.582 | 29.46 |
Kepler found a mathematical relationship between a (average distance to the sun) and P (sidereal period)
Kepler's Third Law of Planetary Motion: Simply P2 = a3
It is easy to verify this for Earth since 12 = 13
We can verify it for any other planet as well. Take Mars for example:
P mars = 1.881 a mars = 1.524
P2 mars = 1.8812 = 3.54
a3 mars = 1.5243 = 3.54
The greater significance of this law will be seen later in this unit. For now, it simply says that if you know how long it takes a planet to orbit the sun, you can then determine its average distance from the sun (in AU). Suppose an astronomer claims to have found a very distant object orbiting the sun. The first question people will want to know is "How far away is it?" If you observe the orbit for some time (the longer the better) ... you can estimate the orbital period by extrapolating. Once the sidereal period is known, you can then apply Kepler's Third Law to estimate the average distance this body is from the sun.
©Jim Mihal 2004, 2014- all rights reserved
Answer: Of course the sun isn't really moving at all along the ecliptic ... it is Earth that is doing the moving. If Earth changes its speed, doesn't it make sense then that the sun will appear to be speeding up or slowing down? Can you guess which time of the year it appeared to be moving the fastest? the slowest? Click here to return.