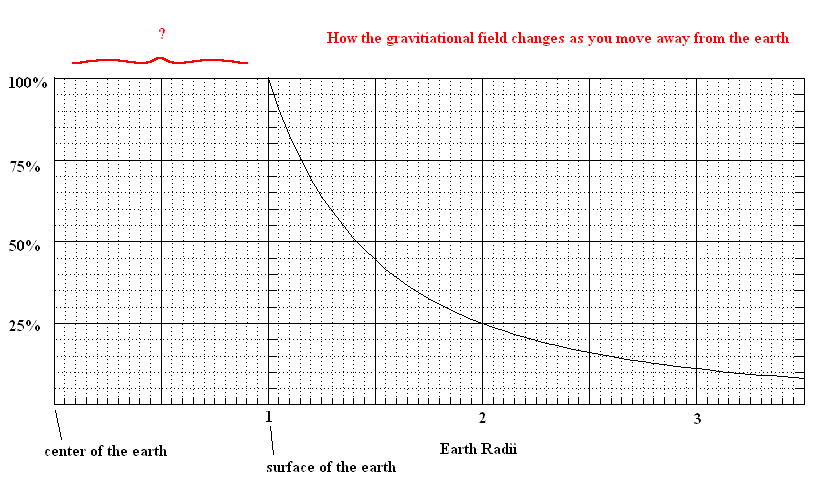
In unit 2, we discuss the "inverse square law", ... showing that gravity gets weaker as you move farther from the earth's surface. The image below shows a graphical representation of this effect.
However, the inverse square law only applies as you move away from the earth's surface. How does it behave as you move below the earth's surface? That is your mission if you choose to answer this topic question.
You get some points if you are able to tell me if it increases, decreases, or just remains the same (compared to surface gravity). You will get all the points if you can offer a logical explanation why this happens. You get bonus points if you find the exact answer. That is, you can describe the curve you would get if you move to left of "1" in the image above. In either case, you must provide some logical reasoning to support your response. The only hint I'll provide is this: What do you think you would experience if you were placed in a box and the box was at the exact center of the earth? You might also want to look at this page (ignoring the math).
This graph is a first approximation and I will accept it as your final answer (providing you explain it properly).
Throw away the inverse square law when you look inside the earth itself. Newton invented calculus to show that the entire earth could be considered a point mass at the center ... but only from a point above the surface Remember that gravity really comes from the each and every particle which makes up the earth. So what happens if you are in an insulated box placed at the very center of the earth? You would "float" in that box! Why ... because you are being pulled to the right just as much as you are pulled to the left. Do you want to call this "weightless"? I would call it a "zero g" environment.
If you move the box slightly off center, you will be pulled slightly more in one side than the other (because there is more earth on one side) ... so you would be pulled slightly toward the center of the earth. The farther you move from the center of the earth, the greater the imbalance ... and the stronger the net force ... the more you would weigh. This continues in a linear fashion until you reach the surface.
This means your weight is the greatest at the surface (just our luck). Your weight drops dramatically as you move above the surface by the inverse square law. If you dig a deep hole in the earth and you climb in, your weight drops also, but in a linear fashion. That is, if you weight 200 pounds at the surface, you will only weight 100 pounds if you go half way to the center of the earth.
There are other ways to analyze this problem. You might start with an idea Newton was able to show ... and that is ... the net force of gravity inside a hollow sphere is zero. That is, if the earth were shaped like a basketball (just the crust but no mantle or core) .. you would float on the inside. Now take that idea and think of the actual solid earth as made up of a whole pile of hollow spheres or "shells" ... one on top of the other (like layers of an onion). If you were at the exact center of the earth, you could apply this idea for each "hollow sphere" and see that your net gravitational force would still be zero. However, if you move away from the center of the earth (but still below the surface), you will be on the inside of some of these shells and on the outside of some others. The shells above you (the ones you are inside of) contribute nothing to your gravitational force. However, all the shells below you (the ones you are outside of) will contribute to your gravitational attraction. The more shells you are outside of, the greater your gravitational attraction. This is why your weight would increase as you move closer to the surface of the earth (from the center).
This is the actual answer and I really don't expect anyone to dig this out but will really be impressed if you find it.
The answer given above assumes that the density of the earth is uniform. The earth is NOT uniform in density. Please look at this picture. It diplays the answer shown above but there are two extra curves. The "linear density" curve shows a model which assumes the density increases in a linear manner as you go deeper inside the earth (which is also not true). But the super technical (and correct) answer is the curve marked PREM. This one is tricky to explain so here goes. The core of the earth is MUCH denser than the mantle above it. So you have to use the reasoning given by the first answer but also think of the core as an additional complication to be dealt with by itself. Let's do that here. Think of yourself as being 1,800 miles above the core (and ignore the mantle altogether). Then you CAN apply Newton's law and say as you move closer to that core, your weight will increase ... reaching the highest value once you reach the core surface (at about .5 of the earth's radius). Now bring into the fact that as you move closer to that core boundary, there is all kinds of mass from the mantle ABOVE you ... and the net result is a curve shown in the graph marked PREM. This shows that your maximum weight occurs at the core boundary and then drops to zero as you reach the center of the earth.