The geocentric universe.
It is really not unusual at all that the ancient Greeks felt the earth as the center of the universe. Most all cultures felt the same way. Much of that belief comes from an egotistical view of the universe ... where man casts himself in the leading role of the cosmic play. The Greeks argued this point, but based their decision on evidence as well! Aristotle argued that the earth must be the center of the universe which we will call the geocentric view. However, we all learn at a very early age that the earth goes around the sun (revolves) and spins on its axis (rotates) ... a model which we call the heliocentric view. The story of how we moved from one viewpoint to the other is a long and interesting story which requires careful analysis which takes us into the next section. For now, we need to see why the Greeks adopted the "earth centered" universe and why it hung on for so many centuries.
It is interesting to know that you can account for all "heavenly" motions (both daily and seasonally) with a geocentric model.
The geocentric universe.
To make the day/night cycle, simply keep the earth stationary, and spin everything around the earth. After all, that is the way it appears! The seasons are a bit trickier. You need two separate spheres centered on the earth. One is the celestial sphere which holds all the stars. The second sphere holds just the sun. Both spheres move around the earth, but with slightly different speeds and each on a different axis of rotation. The sun's orb is tilted 23˝ degrees with respect to the celestial sphere (which can be seen in the image above). To account for the seasons and the apparent motion of the sun along the ecliptic, you need to have each sphere rotate a slightly different speeds. The orb of the sun must lag behind the celestial sphere about 1 degree each day. This way the sun appears to move eastward along the ecliptic ... taking a full year to complete the track. It also accounts for the seasons because of the tilt of one orb to the other. Around June 21, the sun is 23˝ degrees above the celestial equator ... shining over the northern hemisphere. This is reversed on December 22. To account for the moon, a third sphere must be introduced ... and then even more spheres for the planets.
Aristarchus 310 - 230 BC
Almost 1800 years before Copernicus started his "revolution" in astronomy, Aristarchus of Samos was suggesting that the earth orbits around the sun! Essentially he got it right, but was unable to convince his fellow scholars that the universe was put together this way. Why? Aristotle argued against a moving earth because he felt we would leave behind our moon and even the air in the atmosphere as we sped through space. Another argument dealt with the fact that we don't "feel" as if we are moving. These, of course, are invalid arguments in light of modern physics, but fit well in with the science of the day. Probably the greatest argument against a moving earth came from an observation which wasn't noticed - parallax!
If the earth moves around the sun (the Greeks argued), one should observe a parallax effect with the stars on the celestial sphere. That is, when the earth is close to a constellation, it should appear large in the sky and then shrink in size as we move away from that same constellation. This effect was never observed so it became logical to assume that the earth remains stationary in space. This is illustrated in the animation below.
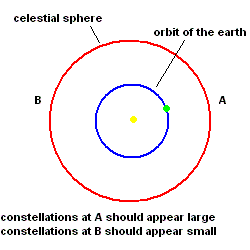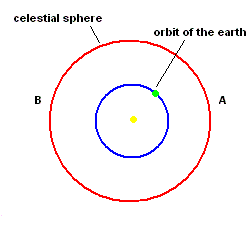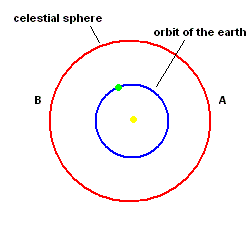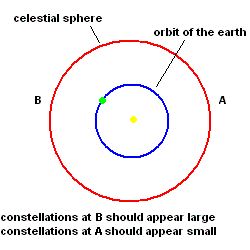
This argument left the Greeks totally convinced that the earth must be stationary in the center of the universe, and Aristarchus' idea of a moving earth was abandoned. Aristarchus contributed to the field in many other ways. Every Greek knew that the sun was farther from us than the moon. Why? During a solar eclipse, the moon passed between the earth and the sun, so it must be closer.
The moon is closer to the earth than the sun.
Both the sun and the moon sustain an angle of ˝ degree in the sky (see the image above), but this really doesn't tell you how much farther the sun is from us than the moon. This was a question Aristarchus attempted to solve. Study the diagram below which shows the geometric arrangement of the sun, earth, and moon when the moons appears half illuminated to us (1st quarter phase). Aristarchus realized that there must be a 90 degree angle at the moon ... forming the famous right triangle you studied in high school geometry. At that exact time, he measured the angle between the moon and the sun ... which locks the triangle to one unique shape. He found this angle to be 87 degrees. Given this value, the sun is then 19 times further from us than the moon. The sun is actually about 400 times further from us than the moon! Why so far off? The actual angle is 89 degrees 51 minutes (not 87 degrees), and it is difficult to know exactly when to take the measurement. Please don't fault Aristarchus for the poor value. This is an idea which is far ahead of his time. As instruments became more accurate, this experiment would yield better and better results. In either case, it was apparent to the Greeks that the sun was much farther from us than the moon and therefore much bigger physically than the moon (since they both sustain the same angular size of ˝ degree).
Aristarchus thought the sun was 19 times farther from us than the moon.
Aristarchus even showed that the moon was 1/3 as large as the earth (which is quite close to the actual value of 1/4). He did this by observing lunar eclipses and comparing the size of the moon to the size of the earth's shadow (at the moon's distance). Even though his geometric arguments are beyond the scope of this project, I hope you can appreciate the brilliant logic and mathematics displayed in this experiment. For example, if the shadow of the earth did not change, it would be quite easy (see image below). Aristarchus had to take into account the fact that the shadow did change as you moved farther from the earth ... making the calculations much more complex.
Aristarchus thought the moon was about 1/3 as large as the earth (actual value
is 1/4)
Aristarchus now believed that:
The moon was 1/3 the size of the earth (actual value was 1/4).
The sun was 19 times farther away from us than the moon (actual value was about 400).
The sun was 19 times bigger than the moon (actual value was about 400).
Therefore, the sun was just over 6 times bigger than the earth (actual value is just over 100).
This led Aristarchus to believe that the sun was the center of the universe! He just could not convince his fellow Greeks due to a lack of observable parallax with the stars.
Aristarchus actually predates the work of Eratosthenes. Once the size of the earth is established, the actual size of the sun and moon can be estimated.
Hipparchus 190 - 120 BC
Probably one of the greatest (and under-rated) astronomers ever to live was Hipparchus of Rhodes. Most textbooks laud the accomplishments of Aristotle and Ptolemy, yet Hipparchus probably did more for the subject than any other Greek. Most of Ptolemy's works were based on his ideas, yet Ptolemy is generally given credit because he perfected most of Hipparchus' ideas. Below is a short list of some of the accomplishments of Hipparchus:
Hipparchus invented trigonometry, a branch of mathematics which
he used to determine geometric relationships between the earth, moon and sun.
The word "tri" (which means 3) comes from the reference to these three bodies.
He made elaborate sky charts which included 1080 stars. On
these maps he invented a coordinate system similar to longitude and latitude on
the globe. Each star was given a number (1 to 6) based on its brightness.
The brightest stars were 1 and the naked eye limit were 6. Our modern
magnitude scale is a slight modification of this original brightness scale.
He used data on eclipses to determine that the moon's distance
from us was 59 times the earth's radius (actual value is 60). This
involved clever use of logic and intricate mathematics ... and is beyond the
scope of this project. Ptolemy used a different (more direct)
technique and arrived at the same number. Most textbooks give all the
credit to Ptolemy.
Hipparchus could tell you the duration of a year to within 6
minutes.
He determined the motions of the sun and the moon so well that
he could predict eclipses within a few hours.
By studying sky maps made generations earlier, he was able to
detect the precession of the equinox.
He perfected the sun's motion along the ecliptic so well that he observed slight irregularities in its speed. At one time of the year it seemed to go slightly faster, at other times slightly slower. Use your SC001 sky charts and pick out a few 10 day intervals along the ecliptic throughout the year. With careful measurements, you should be able to see this effect. Why is this significant? Once you see how Hipparchus solved this mystery, you will understand how Ptolemy used the same techniques to construct his model for the entire solar system.
Hipparchus had to account for the irregular speed of the sun along the ecliptic which he discovered. At this time, it was believed that all heavenly bodies were perfect spheres. Not only that, but any sphere in motion must revolve with uniform speed. This is just the opposite to what Hipparchus discovered. He needed to mend this inconsistency ... and he did.
Method #1 - The Eccentric
One way to keep the heavenly spheres spinning with uniform speed and appear to speed up or slow down is by moving the earth "off center". When the sun is farther from the earth, it only appears to go slower ... when the sun is closer to the earth, it appears to go faster. Although Hipparchus preferred this method, several Greeks objected because it removes the earth from the "center of all things". Later Ptolemy had to re-introduce this idea to perfect his planetary model.
The Eccentric
Method #2 - The Epicycle
An alternate way of solving the same problem is to place the earth back to the center of the universe and move the sun. We need two spheres ... a much larger one (known as a deferent) and a smaller one that rides "piggy-back" on it called an epicycle. Then place the sun on the circumference of the epicycle. All spheres spin at a uniform speed, but the combined motions of both spheres can create the illusion of varying speed (as seen from earth). Study the animations below to get a feeling how this system worked. By changing both the size of the epicycle and the rate that it spins, you can simulate many types of irregular motions.
|
Slow moving sun (animation) |
Fast moving sun (animation) |
Ptolemy 87 - 150 AD
Over 200 years pass in Greek astronomy between Hipparchus and Claudius Ptolemy of Alexandria. Ptolemy basically took all of Greek astronomy and summarized it in his great book - The Almagest (which means The Greatest) which consisted of 13 volumes and became the "astronomical Bible" for centuries. In it, he expanded on all the great works of earlier astronomers and added some "finishing touches" to the geocentric model. In his honor, the geocentric model is often referred to as the Ptolemaic model.
Ptolemy used a method of triangulation to find the distance to the moon. Two observers, both looking at the moon at the same time, are able to calculate its distance provided accurate date is taken at the time. He was able to arrive at the same value as Hipparchus ... which was 59 times the radius of the earth (modern value is 60). The formula for finding the distance is: d = 57.3 * AB / θ where AB is the distance between the two observers, and θ is the parallax angle in degrees.
Using parallax to find the distance to the moon.
Until now we have ignored the movement of the planets along the celestial sphere ... and for good reason. Their motion is highly irregular, and none of the Greeks prior to Ptolemy could adequately explain their motion. The sun and moon always move in the eastward direction with respect to the stars, and so do the planets ... most of the time. Each planet exhibits a very odd behavior when they stop and start moving westward against the stars. When they do that, they are moving retrograde. This happens for a short time, and then the planet returns to the normal eastward motion. The animation below shows this phenomena.

Retrograde motion of Mars (animation)
If possible, view this 703 kb video in AVI format which shows the retrograde motion of Mars - click here. I also have a much better animation but the file is large .wmv format (2 MB) OR .mp4 format (1 MB).
So how did Ptolemy solve this mystery? He "borrowed" an idea from Hipparchus and used epicycles. The animation below shows how you can explain the retrograde motion of Mars by placing mars on an epicycle with the correct size and spin to make Mars "appear" to move backwards (as seen from earth).
Retrograde motion using epicycles (animation)
Ptolemy found the motion of the planets so irregular, he was unable to satisfactorily plot their motions with one epicycle apiece. He invoked an idea (similar to Hipparchus' eccentric) which he called the equant which moved the earth from the true center of universe. He was even forced to place epicycles on top of epicycles to eventually describe the observed motions of the planets. This system worked, but it certainly was NOT simple!
Here is a glimpse of the entire Ptolemaic Universe which still holds the record as the longest held theory in science. Ptolemy made no attempt to assign actual distances to the planets.

Two significant events should be noted before we move to the next section which is the renaissance of astronomy.
None of the original Greek writings have survived the ages. Fortunately, we have the Arabic cultures to thank for preserving the discoveries made by the Greek culture and keeping interest alive in the subject. These Arab cultures included the Chaldaeans (Babylonian astronomers), and Mesopotamian civilizations. It is interesting that the Arab cultures assimilated the constellations from the Greek/Roman society, but renamed many of the stars into Arabic. We still use this system in the western culture. Here is a short list of the proper names of some bright stars (notice the distinct Arabic identity): Aldebaran, Altair, Betelgeuse, Deneb, and Vega.
Another event in astronomy dealt with the rise of Christianity in the western culture. Once Rome fell, the Catholic Church came to power and adopted the Ptolemaic model as Christian doctrine. One reason for adapting this model may have come from the pure respect all scholars had for it. Perhaps the Church felt it would receive the same respect if it embraced this system. A more plausible reason comes from text found in the Bible.
Psalms 93:1 The LORD reigns, he is clothed with majesty; the LORD is clothed with strength, wherewith he hath girded himself: the world also is established, that it cannot be moved.
... also in the book of Joshua
Joshua 10:13 And the sun stood still, and the moon stayed, until the people had avenged themselves upon their enemies. Is not this written in the book of Jasher? So the sun stood still in the midst of heaven, and hasted not to go down about a whole day.
These scriptures were taken as evidence that the sun (not the earth) is moving in accordance to the Ptolemaic system. Once a model moves from a scientific arena to become a statement of religious doctrine, all the rules change! It no longer becomes a question for debate (at least not then). This ensured that the Ptolemaic system was not going to be seriously challenged. The penalty for heresy was typically death. For example, Giordano Bruno declared that the stars might not be at the same distance (on the celestial sphere) from us ... but rather, at many different distances throughout space. He even speculated there might be life on other worlds. Soon afterwards (in 1600 AD), he was burned at the stake (especially since he refused to accept the divinity of Christ).
Now you can understand the challenges scholars of the middle ages had if they proposed to challenge the common beliefs.
ŠJim Mihal 2004, 2014- all rights reserved