The celestial sphere shows no depth. That is, you can not tell how far away anything actually is in the sky (using the naked eye). You can determine the separation of objects ... in degrees. A full circle measures 360 degrees, so the celestial sphere extends 180 degrees from one horizon to the opposite horizon. Ancient observers used astrolabes, cross-staffs, and sextants to measure the angular separation between two objects. You can get close using nothing but your hand.
|
|
|
If you extend your arm and make a fist, the fist itself extends an angle of about 10 degrees. Your pinky finger will extend an angle of about 1 degree. Using this technique gives you a feeling for angles in the sky. Do you think your little finger (with arm extended) will "cover" the full moon? Make a guess and then click here to find the answer.
Keep in mind that the angle you find really says nothing about the physical size of the object you are observing. The full moon and the sun sustain the same angle in the sky but are definitely NOT the same size.
|
still image |
animation |
The image shows that the blue sphere and green sphere sustain the same angle to the observer. In order to do this, the larger sphere must be farther away. From this information alone, the observer could not tell which was physically bigger or smaller ... or which was closer or farther (unless one crosses in front of the other).
Astronomers are able to measure very small angles in the sky ... much smaller than 1 degree. To accomplish this, each degree is subdivided into 60 arc-minutes ... so 1 arc-minute is 1/60 of a degree. An angle of 1 arc-minute is designated as 1'. The diameter of a quarter 287 feet away will extend an angle of 1 arc-minute ... yet astronomers (Tycho Brahe) were able to obtain accuracy of 1' - 2' before the invention of the telescope in their observations.
Measuring even smaller angles are possible (using telescopes), so even a smaller unit is needed. If one subdivides an arc-minute into 60 equal parts, each division is an arc-second (designated 1"). If you hold a quarter 3¼ miles away, its diameter would extend an angle of 1" (one arc-second). Actually measuring to this accuracy might sound pretty impressive, but instruments (such as the VLBA) have achieved accuracies of a fraction of a milliarcsecond. You would have to place that quarter over 1,000 miles away to sustain this angle!
Review:
360 degrees = full circle
1 degree = 60 arc-minutes
1 arc-minute = 60 arc-seconds
1 degree = 3600 arc-seconds (60 x 60)
So far, we have assumed that you are observing the sky from a stationary location. However, that is rarely the case.
Consider the animation below:
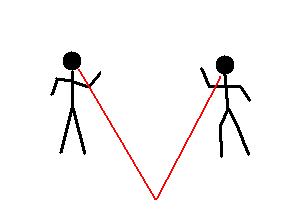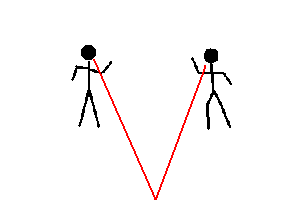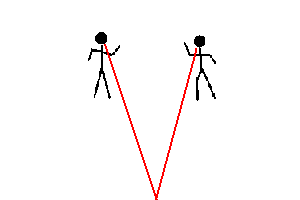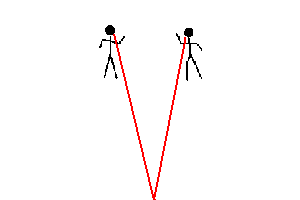
Moving away from two friends (animation)
If two friends remain stationary and you move away from them, there are two changes you will notice as a result ... your friends seem to get tinier, and they move closer together. Of course, this is an illusion ... caused by your motion. This is just one example where your perception of things change because YOU are changing .. and is known as parallax.
|
|
|
Hey, who moved my stuff?
You will see another example of parallax when you observe the two images taken seconds apart from my backyard. There are different ways to interpret these images ... either someone re-arranged things in my yard between pictures .... or the pictures were taken from a different location ... or both. It seems unlikely someone moved the basketball pole or transplanted the tree behind it. OK ... I moved! You can observe the same effect if you extend your arm and hold up your thumb as if you were hitch-hiking. Now close one eye and look at your thumb with the other. Without moving your hand, look at your thumb with the other eye (only). Your thumb moves ... at least it appears to move! This is parallax and something all astronomers must consider when observing the sky. Are we moving or is "it" moving?
Parallax can be a very useful tool when someone wants to determine the distance to an object. You do it every day! We have two eyes so we can observe the universe from two different perspectives. Our brains are wired so we can instantly observe the world around us and calculate the distance to nearby objects with ease. To test this, have someone toss you a ball and try to catch it ... no problem (I hope). Now try it again with one eye closed ... much more difficult. Our two eyes give us depth perception. You should even be able to estimate how far from the camera my basketball is (in the images above). Note: you can even do this with just one picture (because you have a pre-conceived notion how big all basketballs should be).
Astronomers throughout the ages have used this same technique to find the distance to "nearby" objects in the sky. In class or in a discussion topic we will investigate this method of finding distance.
Why can't we use our eyes to find the distance to the moon? The moon is so far away that the tiny displacement of our eye sockets is not enough to show any parallax for the moon. Beyond a certain distance, our eyes lose all depth perception because the more distant the object, the smaller the observed parallax. One way to overcome this problem is to use two observers ... very far apart ... both observing the same object at the same time. With careful observations and geometric data, you can triangulate to get the distance to remote objects. Surveyors have done this for centuries and so have astronomers.
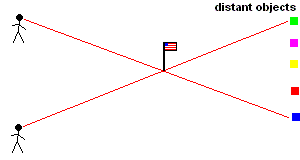
Surveyors triangulate to find distance
It should be clear to you that even triangulation has its limits. That is, surveyors (and astronomers) reach the limits of their instruments, and this technique no longer becomes useful.
If interested, click on this link or this link which lets you see a parallax applet.
©Jim Mihal 2004, 2014- all rights reserved
Answer: The full moon extends an angle of ½ degree in the sky (so does the sun ... but please do not try this technique with the sun ...one false move and you could injure your eye). If you extend your arm, your little finger is more than enough to "eclipse" the full moon. Most everyone gets this one wrong. Click here to return to the web page.