Modern man has always tried to find order in this chaotic universe. One way to gain a sense of control was to decipher the patterns or cycles that occur in the sky. Certainly, two cycles were obvious, seasonal patterns and lunar cycles. Calendars were constructed from these cycles so people could predict events (when to plant, when it will flood, etc) and to know when to celebrate important events (mostly religious events). There are literally hundreds of calendars in use today. In this unit, we will only trace the roots of our modern calendar in any detail.
Calendars typically come in three different forms:
Solar Calendars which are based on seasonal cycles alone
(our modern calendar - the Gregorian Calendar)
Lunar Calendars which are based solely on the lunar cycle of phases
(Islamic Calendar)
Solar-Lunar Calendars which combine the two mentioned above (Jewish
Calendar)
Our modern calendar has evolved throughout the ages, and pieces of that story still remain. The roots of the Gregorian calendar start with the ancient Greeks and Romans. The early Greeks originally used a Solar-Lunar calendar to measure the passage of time. The month (moonth) was designed to keep track of the moon ... which takes 29½ days to complete its cycle of phases. The solar (seasonal) cycle took about 365¼ days to complete. The problem was to design a calendar which could account for both cycles at once. Their solution to this problem was interesting. Since you can not divide a day into parts, the month was either 29 (which they called empty) or 30 days (which was called full). The year contained 6 empty months and 6 full months and each month started at the beginning of the lunar cycle. This worked well for the moon, but not so well for the seasons because a full year would take only 354 days to complete (not even close to 365¼). The way around this problem was to add a "leap month" every now and then. If you added 3 of these extra months every 8 years, the calendar would match up well with the solar (seasonal) cycle. However, this early calendar was not easy to administer because there were no set rules as to when these "adjustments" were to occur. Various attempts to reform this solar-lunar calendar failed, ... a new approach was needed.
In 45 B.C., emperor Julius Caesar scrapped the lunar part of the calendar altogether and declared that the calendar would be strictly solar. In order to avoid dividing a day into fractions, the system was actually quite simple - each year would be 365 days long with every 4th year having 366 days (or leap year). This averages to the required 365¼ days.
One remnant of this older calendar was the months. It no longer has any connection with the lunar cycle (notice a lunar cycle can occur anytime in a month?) ... but it also means you can "stretch" them out so the year contains 365 or 366 days. If you are the emperor, you even get to name a month after yourself (and make it last 31 days) - July. August Caesar did the same thing.
Ever wonder about some other months? September was named for the prefix "septum" .... meaning 7th, October for "octum" ... meaning 8th, November for "novum" or 9th, and finally December for "decum" ... the 10th month. What is that all about? Isn't December the 12th month? December was originally the 10th month of the year because the beginning of the calendar coincided with the spring equinox (which occurs in March). The Romans moved the start of the calendar to January because they felt their annual senate meetings were that important.
Every 4th year we have a 366 day year known as a leap year. It was added to an already short month, February. So every 4th year we can find a February 29th on the calendar. Any year that is evenly divisible by 4 is designated a leap year. Still have your 2004 calendar around? Then look for that extra day. Which brings up an interesting question - why is it called a "leap" year? If every year had just 365 days, you would find that your birthday would advance one day ahead each successive year. That is, if your birthday occurs this year on a Monday, the next year it occurs on a Tuesday .... unless it crosses over a February 29th ... in which case it "leaps" over a day and occurs on a Wednesday.
The Julian Calendar worked great, but it wasn't perfect. To see why, you need some details.
The actual length of the seasonal cycle is called a tropical year, and lasts 365.2422 days. The technical definition for a tropical year is the time between two successive crossings of the sun against the Vernal Equinox. That is, start when the sun is on the Vernal Equinox ... let it move along the ecliptic ... and stop when it gets back to the Vernal Equinox. This is actually just a "tad" short of a complete revolution around the sun because of precession. That long 26,000 year wobble of the earth's axis means the Vernal Equinox does not stand still ... so as the sun is moving eastward along the ecliptic, the Vernal Equinox is moving slightly westward. They meet again 1/26000 short of a full revolution. The good news is that any calendar based on a tropical year will always match up with the seasons.
Since the goal of any solar calendar is to average 365.2422 days, you can see that 365¼ is just a bit too long. The difference is only 11 minutes and 14 seconds and too small to worry about ... unless the calendar is in effect a very long time. By 1582, this small difference accumulated to a full 10 days! This meant that the sun was crossing the Vernal Equinox around March 10th instead of March 20th. Pope Gregory XIII decided this was too much error and called for a reform to the calendar.
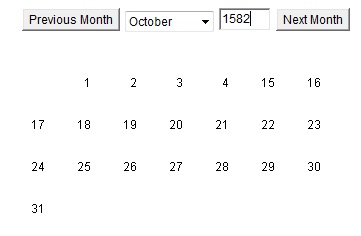
The Pope actually made 2 reforms to the calendar in 1582. The first was to correct for this error of 10 days. It was declared in 1582, that October 4th was to be followed by October 15th. This eliminated 10 days, bringing the sun back to the Vernal Equinox on March 20th. If you click on this java based perpetual calendar and look at the month of October in 1582. This is what you will see:

The second adjustment the Pope made was to eliminate the error so it would not need further corrections. To shorten the average length of a year from 365.25 days down to 365.2422 days, certain planned leap years would be eliminated. You don't need to eliminate many ... so the plan was: any century that can not be divided evenly by 400 will have the first leap year of that century eliminated. Go back to the perpetual calendar and look at February in these years - 1600, 1700, 1800, 1900, 2000, 2100, etc. Notice which years do not have a February 29th. You will discover that you will not live long enough to experience the next "Gregorian correction". I would imagine there will be a lot of confused folks in February, 2100 .... wondering where their leap year went????
Personal note: Not everyone embraced this reform to the calendar. My grandfather was raised Eastern Orthodox, which means if the Pope says go left, you go right. As a child I was often mystified why we would celebrate "Grandpa Christmas" on January 7th each year. We just figured Grandpa was cheap and got after Christmas bargains. Later I found it was because he celebrated Christmas (December 25th) on an old Julian Calendar.
The concept of a week has been around for a very, very, long time. When I ask my class why the week was formed and why it is subdivided into seven parts, references to the Bible usually are mentioned (see the book of Genesis). The reason we have a week most certainly has something to do with religion but not necessarily with Christianity. The first hint comes from the names we give each day. Modern English names for each day came from the Norse language.
Sunday - for the Sun
Monday - Moon day
Tuesday - Tiw, the Norse God - Mars. You see this better if you
know French (mardi) or Spanish (martes)
Wednesday - Woden, the Norse God - Mercury.
You see this better if you know French (mercredi) or Spanish (miércoles)
Thursday - Thor, the Norse God - Jupiter.
Friday - Freya, the Norse Goddess - Venus. You see this better if
you know French (vendredi) or Spanish (viernes)
Saturday - The Norse God - Saturn
As you can tell, each day was dedicated to honor these Gods in the sky.
©Jim Mihal 2004, 2014- all rights reserved