Every great ancient civilization studied astronomy for reasons stated in the very beginning of this project. You could spend an entire semester dealing with just this subject (as I once did as a student). One culture stands head and shoulders above all others when it deals with this subject - the Ancient Greeks. Why? Perhaps it stems from the main reason they studied astronomy in the first place - a philosophical desire to learn about the universe we live in ... within an academic setting which allowed differing viewpoints. Since we have limited time to explore this topic, we will ignore the considerable accomplishments of other cultures (Egyptian, Babylonian, Chinese, Native American, etc) and concentrate on the endeavors of the ancient Greeks.
Pythagoras-
We have very little knowledge of his life. He was born around 569 B.C., and died sometime near 475 B.C.. He is best known in the field of mathematics for his famous equation dealing with right triangles: a2 + b2 = c2 which is known as the Pythagorean Theorem.
In the field of astronomy, Pythagoras taught that Earth and all heavenly objects were spheres. He reasoned this by looking at the moon. The light shining on the moon comes from reflected sunlight ... the moon merely acts as a projection screen. He observed that there is a curve to the zone between light and dark (the terminator) when it approached the edge of the moon. Only a spherical object would produce this curvature. If the moon were a sphere, must not all heavenly objects (including Earth) be spheres?
Aristotle (384-322 BC)
Aristotle added more evidence to support a spherical Earth model by observing lunar eclipses. During a lunar eclipse, the shadow of Earth is cast on the moon. Aristotle noted that the curvature of the shadow showed remarkable consistency. That is, under similar situations in the past, all eclipses produced the same curvature ... which could only happen if Earth itself were a sphere. Note: Observing this curvature during one isolated eclipse proves nothing. A flat penny will produce a circular shadow if held properly in sunlight. The same penny will, however, produce an entirely different shape if rotated 90 degrees to the sunlight (see the animation below). Only a sphere shows a consistent curvature ... therefore, Earth must be a sphere!

The curvature of Earth's shadow during an eclipse
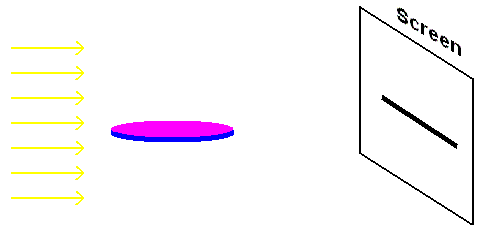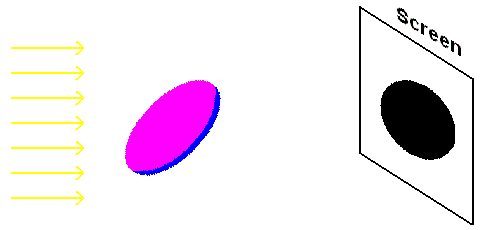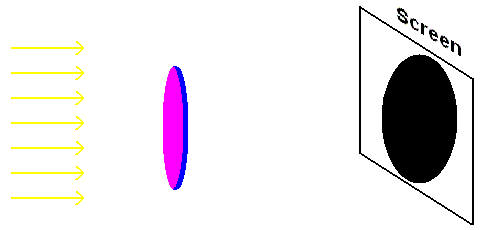
If Earth was shaped like a pizza, its shadow would change (as in this animation).
Another observation attributed to Aristotle supported a spherical Earth hypothesis. As the Greeks moved to new lands (both north and south of Greece), they observed changes in the sky such as changes in the altitude of stars (with respect to the horizon) and even new stars appearing in the local horizon which were not visible from their home land. This, Aristotle argued, showed Earth could not be flat since all observers on a flat Earth have exactly the same local horizon.
spherical Earth flat Earth
To help see this, consider two models. On a spherical Earth, the red stick man and blue stick man have different local horizons (red and blue lines). Red stick man can see "A" but not "B". Blue stick man sees "B" but not "A". On a flat Earth, whatever red stick man sees, so does blue stick man.
So the question is .... are members of the Flat Earth Society really serious? A representative boasted "our followers are located all around the globe" !!!!!
Eratosthenes (276-195 BC) -
Eratosthenes is given credit for finding the size of Earth. This incredible feat is accomplished from a simple observation about the sun in two distant cities, Syene (now Aswan) and Alexandria. On the day the sun crossed the summer solstice in Syene, it appeared at the zenith (at high noon), but was found 7 degrees from the zenith in Alexandria. Eratosthenes realized that through simple geometry, he could estimate the size of the entire Earth if he knew the distance between these two cities.
How Eratosthenes found the size of Earth.
Eratosthenes knew that the sun was far enough away to assume that the rays arrived parallel to each other in both cities ... labeled "A" and "S" in the diagram above. Since the sun appeared 7 degrees from the zenith in Alexandria, he knew that the Syene-Alexandria distance represented 7 degrees (out of 360 degrees) along the circumference (as measured from the center of Earth ... see the diagram above) ... or 1/50th the circumference of Earth. He commissioned a foot soldier to cross the Sahara Desert ... counting his footsteps along the way in an effort to accurately measure this distance! Distances were measured in "stadia" in that era and his measured value for the Syene-Alexandria distance was 5000 stadia. A simple ratio allows you to derive the circumference of Earth as follows:
This yields a circumference of approximately 250,000 stadia ... unfortunately, the exact value for a "stadia" is in doubt. A stadia was the length of the track in the Olympic stadium ... which varied from city to city (much like baseball parks do today). Regardless which standard Eratosthenes used, his estimate was still extremely close (within a few percent) to the modern value for the size of Earth.
ŠJim Mihal 2004, 2014- all rights reserved