
(animation)

(animation)
Stars twinkle because of an atmospheric effect known as scintillation. If you were to observe the stars from above our atmosphere, most would shine with a steady light. However, some stars exhibit light outputs which vary, getting slightly brighter and dimmer with time. These stars are known as variable stars. Stars are variable for a number of different reasons, and each reason gives us valuable information about the stars themselves.
Our sun is in the minority as far as stars go. A little over half the stars in the sky have binary companions. That is, they have another star going around it. Sometimes a system has several stars, ... all moving in complex orbits. For example, in the last unit we showed a list of the closest stars, but Alpha Centauri was NOT at the very top of the list. Most books list Alpha Centauri as the closest star to us because of the 3 stars in the system, Alpha Centauri is most like our sun. In this system, two rather massive stars orbit close together (A & B), ... and a much less massive star (Proxima Centauri) orbits around the pair. Currently, Proxima is physically the closest to us.
| Name | Distance (ly) |
| Proxima Cen | 4.24 |
| Alpha Cen A | 4.34 |
| Alpha Cen B | 4.34 |
If the orbits are aligned just right in space, one star eclipses the other (as seen from Earth). These are called eclipsing binaries. This short video shows the effect of eclipsing binaries. As one star covers the other, it robs us of the light we would normally receive, and we observe a drop in the total light intensity from the system.
The most famous eclipsing binary is the star Algol (β Persei), named the "demon star" by the Arabs because they observed that it would drop about 3 magnitudes in brightness with a period of just under 3 days. Below is the light curve of Algol.
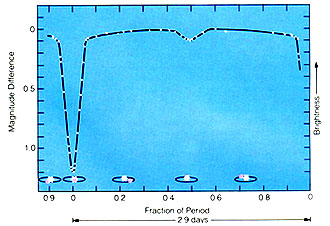 Courtesy NASA |
 Binary star (Algol) animation courtesy Wikimedia Commons |
Binary stars give astronomers the ability to learn quite a bit about the properties of stars. Two stars in a gravitational dance are governed by the same laws throughout the universe. In a previous unit, we showed how the total mass of a system can be determined by applying Kepler's 3rd law (as amended by Newton).
Remember this equation? (m1 + m2) P2 = k a3
By observing the sidereal period (P) and semi major axis (a) of individual stars in a binary system , the total mass of the entire star system can be calculated. To determine how this mass is divided between the two stars, just observe how each star moves relative to the center of mass. If one star has much more mass then its companion, it will behave much like Earth-moon system, where Earth "wobbles" a bit and the moon swings broadly around the center of mass. If the two stars have nearly equal masses, they perturb each other equally. Both stars will always be about the same distance from the center of mass.
If the binary stars are aligned so they also eclipse each other, astronomers can even determine the physical diameters (size) of each star. Consider two eclipsing binary stars shown below. As one star eclipses the other, the light curve takes shape (see animation).
|
|
animation |
The transition from "B" to "C" depends on:
Working backward, astronomers can get the physical distance from "B" to "C" ... or the size of the star.
Imagine how the light curve would change if you were to make the background star twice as large. Also, the transition from "A" to "B" depends on the physical size of the foreground (red) star. Imagine how the light curve would change if this small star were even smaller.
What if a star does not have a binary companion. Does that mean you have no idea how big it is? Fortunately, astronomers have a variety of techniques to estimate the physical size of stars. Outlined below are a few.
Care for some details? The luminosity of a star (L) is related to its radius (R) and temperature (T, ...expressed in Kelvin) by this function:
L α R2 *T4
This means if two stars have the same radius (R) but one is 3 times the Kelvin temperature as the other (say 4,000 K vs. 12,000 K), the hotter star emits 34 or 81 times the amount of light as the cooler star. In another example, consider two stars which have the same temperature, but one is 5 times larger than the other. The larger star emits 52 or 25 times the amount of light as the smaller one. Knowing this relationship, astronomers are able to calculate the radius of any star (compared to our sun) if you know the star's luminosity and temperature. Will you have to do this? No.
Sometimes stars vary their light output because they pulsate. By doing so, they change both their radius and temperature, ... both of which change the luminosity. Most of these stars are very old (dying) and/or unstable stars which represents a short episode in the stars entire lifespan (don't we all go through unstable times?). Astronomers classify them in classes such as Mira variables (which our own sun will eventually reach), RR Lyrae Stars, or Cepheid variables.

pulsating star (animation)
This class of star undergoes very slight changes in brightness over regular intervals. The North Star (Polaris) is a Cepheid variable. With careful observations, the brightness varies slightly (between +2.1 and +1.9 in apparent magnitude) over a period of just under 4 days. Cepheid variables are particularly interesting because they provide astronomers with a valuable tool for determining distance. How?
It was found that the rate at which these stars pulsate is linked to their intrinsic brightness. This is known as the period-luminosity relationship and is depicted graphically below.
As it turns out, this is a major and very important discovery for astronomers. Why? Basically, it is a way of obtaining the absolute magnitude of a star via indirect means. Stars (unlike light bulbs) don't have a stamp on them announcing how much light they put out. However, the period-luminosity relationship gives you this information by measuring their "flicker rate".
To help see how this works, let me give an analogy. Imagine that all light bulbs fluctuated slightly in brightness (they don't really). Light bulbs with low wattages would fluctuate with fast periods and bulbs with higher wattages took longer times to twinkle (as illustrated in the animation below). Instead of simply reading the wattage stamped on the bulb, you could determine it by observing their "flicker rate".
|
|
|
Cepheid stars are like these flickering light bulbs. If the wattage is low, they oscillate quickly. High wattage bulbs take a longer time to go through this cycle (animation)
How does this lead to the distance? Study the example below. Suppose an astronomer observes that a type I Cepheid pulsates with a period of 20 days. Using the chart they could conclude that this star has an absolute magnitude (Mv) of about -5. Why is this important?
|
|
|
Consider the equation below (which was introduced in the last section). It contains three variables - absolute magnitude, apparent magnitude, and distance. By relying on the period-luminosity relationship, astronomers believe they have an accurate value for absolute magnitude (Mv). They can easily measure apparent magnitude (mv) directly. This leaves only one unknown - distance. Using this method, astronomers can estimate the distance to galaxies which may be up to over one hundred million light-years away just by spotting a few Cepheid variables in them.
Do you like to crunch numbers? Suppose in this example the type I Cepheid is observed with a period of 20 days and has a mean apparent magnitude of +5. We already know that the period-luminosity chart predicts an absolute magnitude of -5 for this star. Therefore:
-5 = +5 - 5 log (d/10)
-10 = - 5 log (d/10)
2 = log (d/10)
2 = log d - log 10
2 = log d - 1
3 = log d
d = 10^3 = 1000 pc (which converts to 3,260 light-years)
Don't worry, I will not be asking this kind of question of the test. You should, however, appreciate the gift these stars offer astronomers.
Eruptive Variables
Some stars alter their light output because of intense surface flares or by ejecting a shell of matter from their surface. In other cases, a star may Nova. This occurs in a binary system where one star feeds material to its companion ... initiating a sudden brightening when a critical mass is transferred. More on this later. In the most extreme case, the eruption can destroy the star itself in an event known as a Supernovae or Hypernovae. You can bet this will be covered in much more detail in another section.
In all these cases, the light output varies because the star is undergoing dynamic changes on the surface (photosphere).
Rotating Variables
If a star has intense sunspot activity (much more active than our sun), its light output can change as the light/dark areas rotate from our line of sight.
Transit of a planet
Extrasolar planets have been discovered because they transit in front of the star ... causing a slight but regular decrease in the amount of light we receive. This not only gives information about the planet's existence but also information about any atmosphere the planet might have (see details in unit 3 covering light). This is probably how the first claims of life beyond our solar system will be based (my opinion).
ŠJim Mihal 2004, 2014 all rights reserved